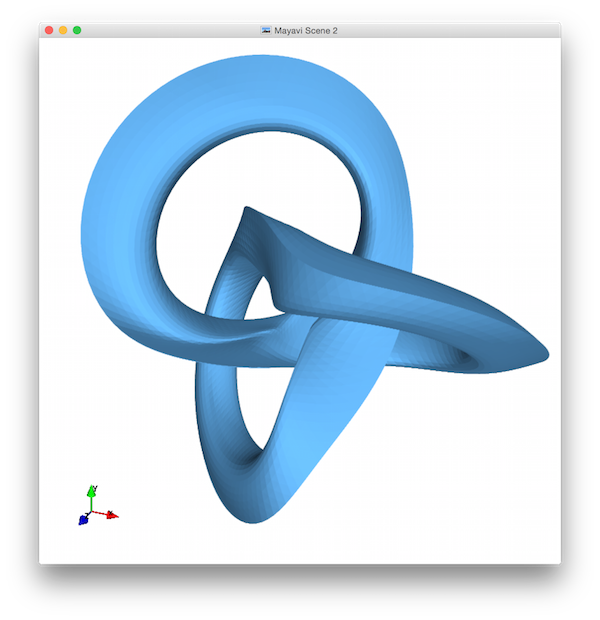
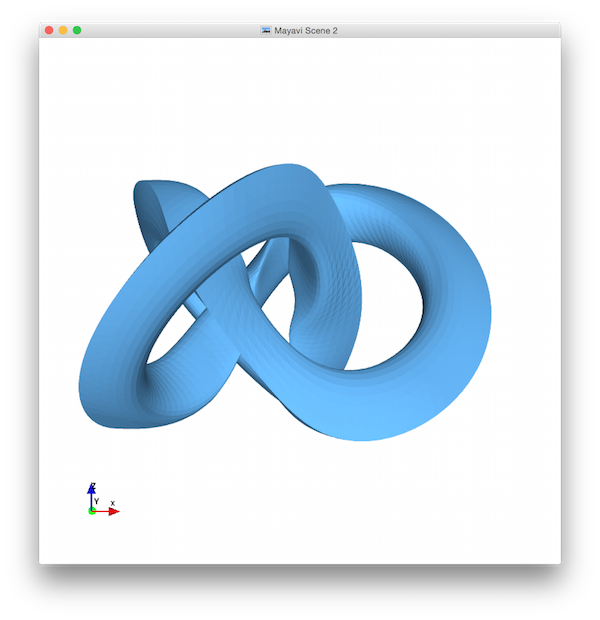
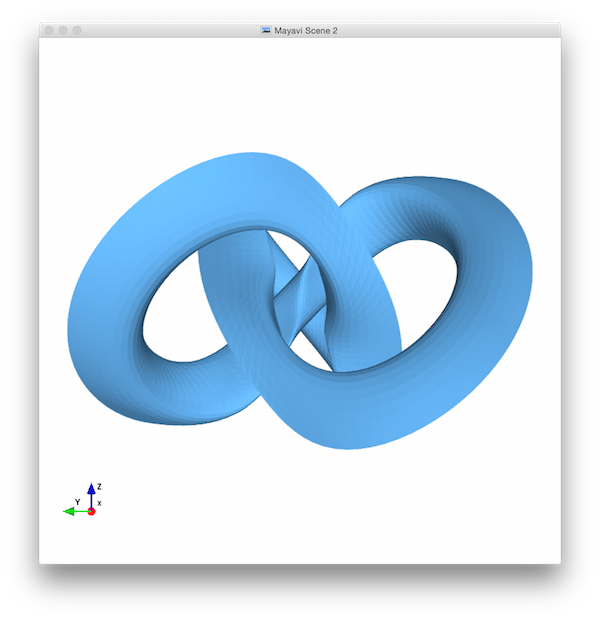
This assignment builds on HW2, in which you constructed vertex sets for a variety of 3D shapes. In this one, you'll create triangle meshes for their surfaces, as well as designing a shape of your own. There are four tasks below:
Download the starter code, meshes.py, as well as the helper file gfx_helper_mayavi.py. As always, there are a number of TODO comments that you should follow, paying attention to the docstrings that define the behavior of each function.
Each function for creating and returning a mesh should call a separate function (like the ones you wrote in HW2) to generate the vertices for it. You may use your own code from HW2 or my HW2 solutions (which I'll post once everyone has submitted theirs). Keep in mind that my solutions may put the vertices in a different order than yours did!
A. Meshes for old shapes
Change the bodies of each of these methods to match their docstrings, and then add calls in main() to display each one in the correct octant:
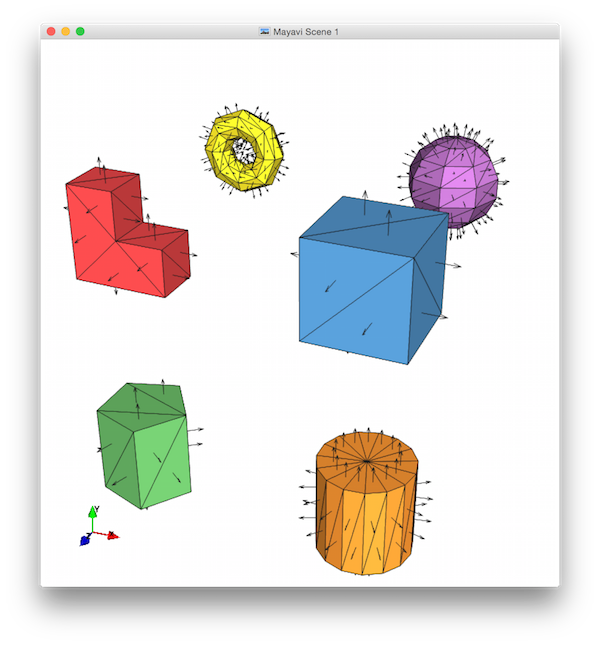
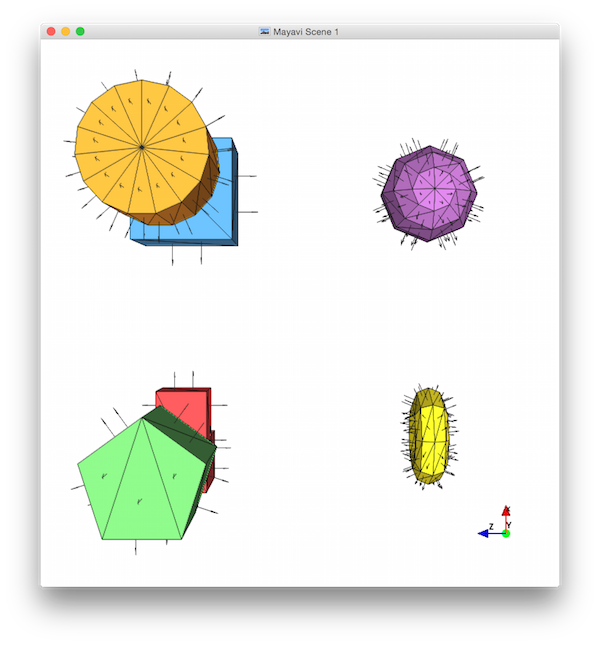
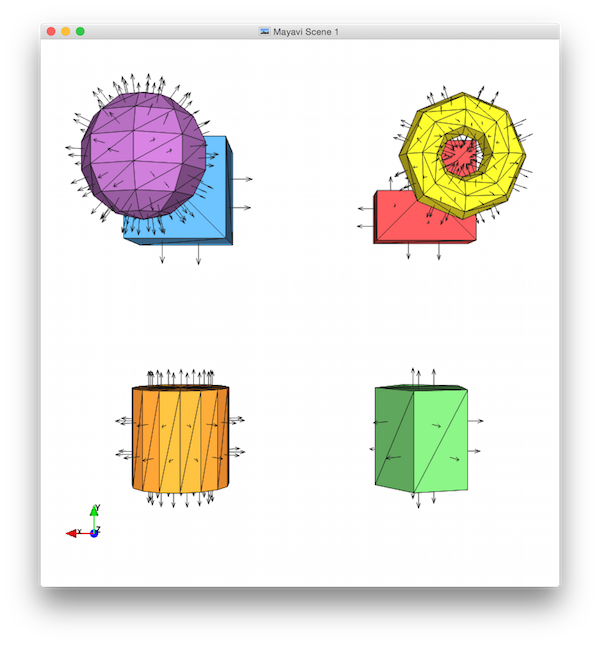
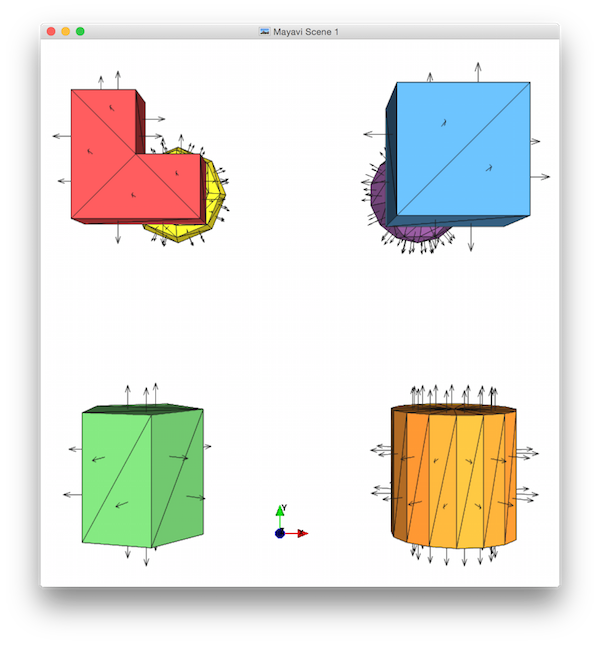
cube()— fill in the body, and display in octant 1 (+++).ell()— fill in the body, and display in octant 2 (-++).prism()— fill in the body, and display a pentagonal prism in octant 3 (--+).- Also display a cylinder (a prism with many sides) in octant 4 (+-+).
sphere()— fill in the body, and display in octant 5 (++-).torus()— fill in the body, and display in octant 6 (-+-).
As always, I'll test your functions with many different values of K (avoiding invalid values or ones that would correspond to degenerate shapes).
Hints
If you'd like, you may modify the behavior of prism() to produce better results for high K values — the example screenshots below show this. Here's an updated signature and docstring that you could use:
def prism(K): """ Returns a 2-tuple (verts, tris) representing a triangle mesh of the surface of a regular K-gon prism. If K <= 6, verts is 3x(2K) and tris is (4K-4)x3; otherwise verts is 3x(2K+2), with an extra vertex in the middle of each end-cap, and tris is (4K-2)x3. (Adding the extra vertex prevents extra-narrow triangles on the end-caps.) See prismVerts(). """
In addition, you may find it useful to define helper functions for building your triangle arrays. By defining these four functions, I was able to build all the triangle arrays just with function calls and array manipulations, without hard-coding any rows of the arrays.
def fanDiskTriangles(K, start=0, flip=False):
"""
Returns a (K-2)x3 array of vertex indices for the triangulation of a K-polygon
in the plane, with indices numbered counterclockwise. Arguments:
- K: number of vertices in the polygon.
- start (default 0): the starting index of the K consecutive indices around
the polygon.
- flip (default False): when False, triangles are oriented right-handed /
counterclockwise; when True, they are left-handed / clockwise.
"""
def wheelDiskTriangles(K, hub=0, start=1, flip=False):
"""
Returns a Kx3 array of vertex indices for the triangulation of a K-polygon
in the plane, with a central "hub" vertex and K vertices in a loop around it,
numbered counterclockwise. Arguments:
- K: number of vertices around the outside of the polygon.
- hub (default 0): the index of the vertex in the middle of the disk.
- start (default 1): the starting index of the K consecutive indices around
the polygon.
- flip (default False): when False, triangles are oriented right-handed /
counterclockwise; when True, they are left-handed / clockwise.
"""
def indexLoop(idx):
"""
Given a 1-D array or list, returns the same as a 1-D array with element #0
repeated at the end.
"""
def triangleStrip(bot, top):
"""
Given two 1-D arrays or lists (each of length N) of vertex indices (bot and
top), returns a (2N-2)x3 array of indices, each row of which is a triangle in
a zigzagging strip between these parallel sets of indices:
0 1 2 3 4 5
top -> *--*--*--*--*--*
| /| /| /| /| /|
|/ |/ |/ |/ |/ |
bot -> *--*--*--*--*--*
0 1 2 3 4 5
The triangles are oriented so that their right-hand-rule outward directions
are all facing out of the page.
"""
B. Screenshots of old shapes
Take eight screenshots of your shapes, as described below, and put them in your PDF. In each screenshot, the edges and face normals of your shapes should be rendered. In addition, the Mayavi orientation widget should be displayed; if you don't see it, click the “Toggle axis indicator” button in the Mayavi menu bar. Each screenshot should be looking in a different direction:
- An oblique view with the Y-axis pointing up, the Z-axis pointing down and left, and the X-axis pointing right. (This is the default view, matching the diagrams in point_clouds.py.)
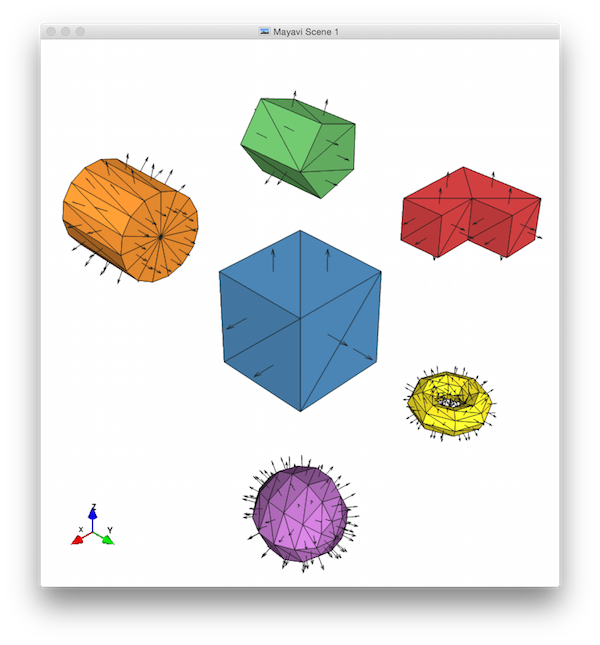
- An oblique view with the Z-axis pointing up, the Y-axis pointing down and right, and the X-axis pointing down and left. (Click the “isometric view” button on the Mayavi viewer's menu bar to get this view — the button looks like a little blue cube.)
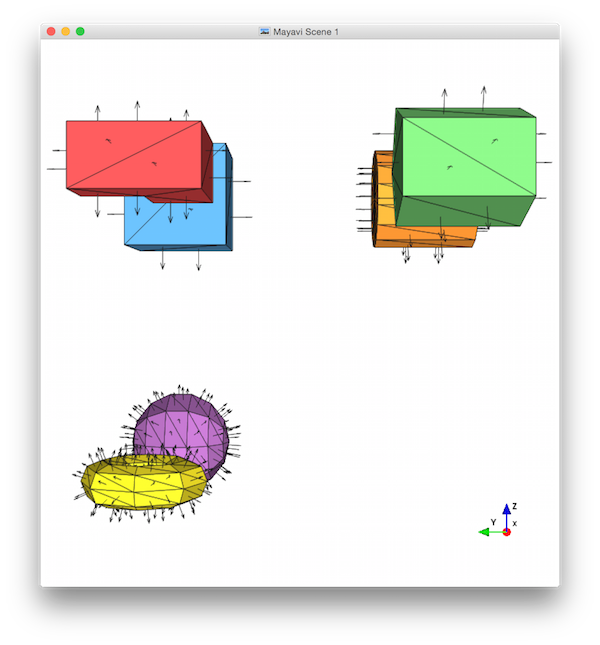
- Looking up the X-axis, with the Y-axis pointing left. (Click the first “X” button on the menu bar.)
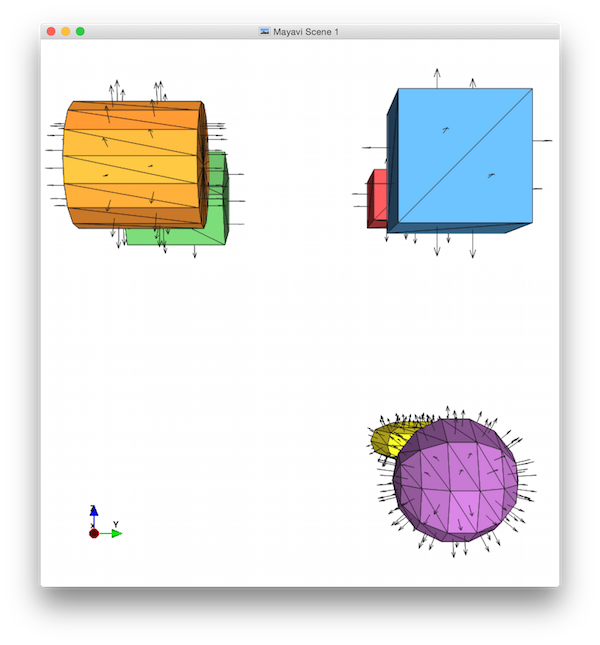
- Looking down the X-axis, with the Y-axis pointing right. (Click the second “X” button on the menu bar.)
- Looking up the Y-axis, with the Z-axis pointing left. (Click the first “Y” button on the menu bar.)
- Looking down the Y-axis, with the Z-axis pointing right. (Click the second “Y” button on the menu bar.)
- Looking up the Z-axis, with the X-axis pointing left. (Click the first “Z” button on the menu bar.)
- Looking down the Z-axis, with the X-axis pointing right. (Click the second “Z” button on the menu bar.)
Here's what these pictures should look like. Notice that I've used a low K-value for the sphere and torus (so the facets and normals are more easily distinguished), that I've implemented the extra prism feature (so there's a vertex in the middle of the cylinder end-cap), that I've zoomed each view in to fill the frame, and that I've moved the orientation widget so that it doesn't cover any of my shapes:
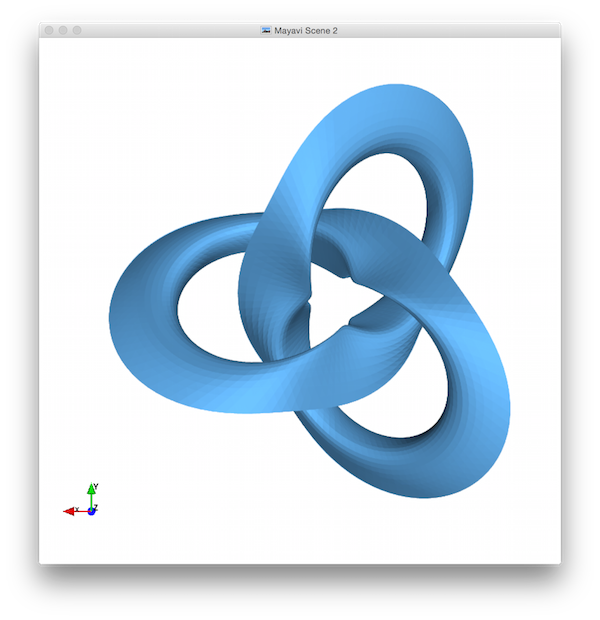
C. Your own shape
Design your own shape that fits within the unit cube. Your shape (and the code you write for it) must have all of these properties:
- The shape must have at least one sharp corner.
- The shape must have at least one curved surface.
- The shape must be water-tight (that is, it must have a distinct inside volume separated from the outside by the triangulated surface you create, with no holes in the surface).
- The functions to generate it must each take at least one argument, specifying the fineness of the sampling of curved surfaces. (Like K in the ones you've done so far.)
- You must write at least two functions: one to generate the vertex set, and one to generate both the vertices and triangles.
- Each function you write must have a docstring, written in complete sentences, with proper punctuation, capitalization, etc., describing its use and semantics.
- The vertex function must be named
my_verts(), and return a 3×N array (for some N). - The surface function must be named
my_shape(), and return a 2-tuple of the 3×N vertex array and an M×3 triangle array. - All your functions must be deterministic and non-chaotic. No random (or pseudo-random) behavior.
In your program, create a new figure that will display after the old one (for step A) is closed, and then display your shape in that, just centered on the origin.
The names must be correct in order to receive full credit. Any shape that meets the specification above (other than a cylinder, which you've already written) will be accepted, but I'd encourage you to get creative!
We'll all share these shapes with each other to use as sample objects in future projects.